对Pytorch神经网络初始化kaiming分布详解
函数的增益值
torch.nn.init.calculate_gain(nonlinearity, param=None)
提供了对非线性函数增益值的计算。
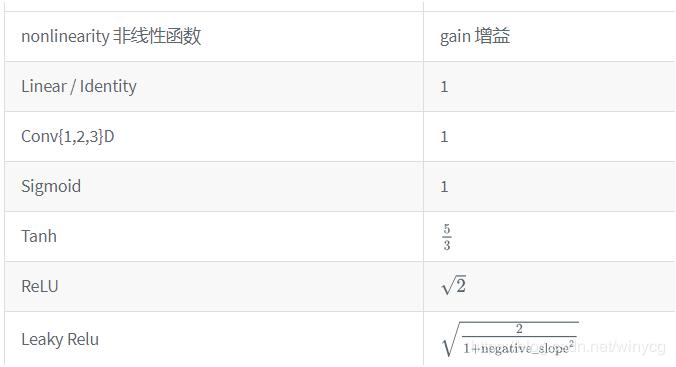
增益值gain是一个比例值,来调控输入数量级和输出数量级之间的关系。
fan_in和fan_out
pytorch计算fan_in和fan_out的源码
def _calculate_fan_in_and_fan_out(tensor):
dimensions = tensor.ndimension()
if dimensions < 2:
raise ValueError("Fan in and fan out can not be computed
for tensor with fewer than 2 dimensions")
if dimensions == 2: # Linear
fan_in = tensor.size(1)
fan_out = tensor.size(0)
else:
num_input_fmaps = tensor.size(1)
num_output_fmaps = tensor.size(0)
receptive_field_size = 1
if tensor.dim() > 2:
receptive_field_size = tensor[0][0].numel()
fan_in = num_input_fmaps * receptive_field_size
fan_out = num_output_fmaps * receptive_field_size
return fan_in, fan_out

xavier分布
xavier分布解析:https://prateekvjoshi.com/2016/03/29/understanding-xavier-initialization-in-deep-neural-networks/
假设使用的是sigmoid函数。当权重值(值指的是绝对值)过小,输入值每经过网络层,方差都会减少,每一层的加权和很小,在sigmoid函数0附件的区域相当于线性函数,失去了DNN的非线性性。
当权重的值过大,输入值经过每一层后方差会迅速上升,每层的输出值将会很大,此时每层的梯度将会趋近于0.
xavier初始化可以使得输入值x x x<math><semantics><mrow><mi>x</mi></mrow><annotation encoding="application/x-tex">x</annotation></semantics></math>x方差经过网络层后的输出值y y y<math><semantics><mrow><mi>y</mi></mrow><annotation encoding="application/x-tex">y</annotation></semantics></math>y方差不变。
(1)xavier的均匀分布
torch.nn.init.xavier_uniform_(tensor, gain=1)
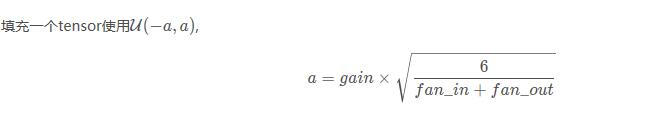
也称为Glorot initialization。
>>> w = torch.empty(3, 5)
>>> nn.init.xavier_uniform_(w, gain=nn.init.calculate_gain('relu'))
(2) xavier正态分布
torch.nn.init.xavier_normal_(tensor, gain=1)
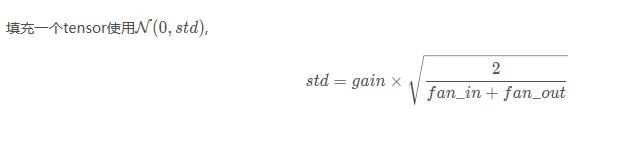
也称为Glorot initialization。
kaiming分布
Xavier在tanh中表现的很好,但在Relu激活函数中表现的很差,所何凯明提出了针对于relu的初始化方法。pytorch默认使用kaiming正态分布初始化卷积层参数。
(1) kaiming均匀分布
torch.nn.init.kaiming_uniform_ (tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')

也被称为 He initialization。
a – the negative slope of the rectifier used after this layer (0 for ReLU by default).激活函数的负斜率,
mode – either ‘fan_in' (default) or ‘fan_out'. Choosing fan_in preserves the magnitude of the variance of the weights in the forward pass. Choosing fan_out preserves the magnitudes in the backwards
pass.默认为fan_in模式,fan_in可以保持前向传播的权重方差的数量级,fan_out可以保持反向传播的权重方差的数量级。
>>> w = torch.empty(3, 5) >>> nn.init.kaiming_uniform_(w, mode='fan_in', nonlinearity='relu')
(2) kaiming正态分布
torch.nn.init.kaiming_normal_ (tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
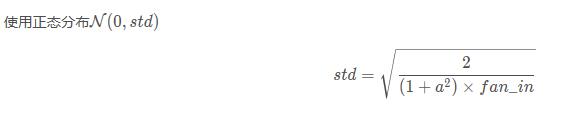
也被称为 He initialization。
>>> w = torch.empty(3, 5) >>> nn.init.kaiming_normal_(w, mode='fan_out', nonlinearity='relu')
以上这篇对Pytorch神经网络初始化kaiming分布详解就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持脚本之家。












最新评论