Python实现归一化算法详情
1.前言
归一化算法Normalization将数据处理成量纲一直的数据,一般限定在[0,1]、[-1,1]
一般在进行建模的时候需要进行数据归一化处理,
原因如下:
- 降低计算难度
- 有可能提高模型的预测精度
- 消除量纲影响
下面介绍三种常见的标准化方法,分别是最大最小值、正态中心化、小数点定标
2.Min-Max方法
2.1 公式
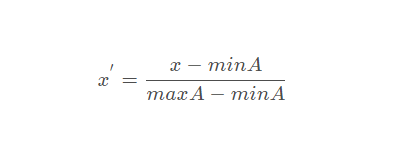
2.2 算法实现逻辑
- 1.找一组数据的最大最小值
- 2.利用公式归一化
- 3.输入结果(为了方便可视化展示,我们设计了代码)
2.3 代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 1.最小最大标准化
Data = np.array([[0.2,0.9,29],
[0.9,0.1,100],
[0.5,0.5,30]]) #最小-最大归一化算法
# 1.1数据转化
def MinMax(data):
min = 0
max = 1
C = data[:,2]
min = np.min(C)
max = np.max(C)
for one in data:
one[2] = (one[2]-min) / (max-min)
print('转化后的矩阵:\n',data)
return data
# 1.2可视化
def ShowData(Data,ShowD1):
length = len(Data)
X = np.ones(Data.shape[0])
plt.figure(1)
plt.subplot(121)
for i in range(length):
plt.scatter(X*(i+1),Data[:,i])
plt.subplot(122)
for i in range(length):
plt.scatter(X*(i+1),ShowD1[:,i])
plt.show()
ShowData(Data,MinMax(Data.copy()))转化后的矩阵:
[[0.2 0.9 0. ]
[0.9 0.1 1. ]
[0.5 0.5 0.01408451]]

2.4局限
- 数据规模过大不适应
- 数据归一化后范围在[0,1],对于一些有负有正数的原始数据慎用
3 Z-score标准化
3.1 公式
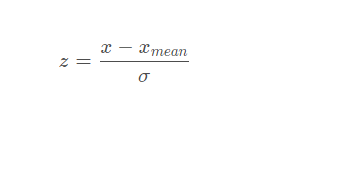
3.2 算法实现逻辑
- 输入数据
- 求取数据的均值、方法,在利用中心化公式计算
- 输出结果
3.3 代码
def Zscore(data):
x_mean = np.mean(data[:2])
length = len(data[:,2])
vari = np.sqrt((np.sum((data[:2]-x_mean)**2))/length)
print('方差:',vari)
data[:,2] = (data[:,2]-x_mean)/vari
print('Z-score标准化后的矩阵是',data)
return data
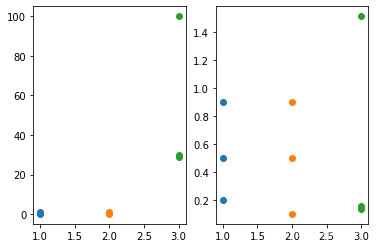
ShowData(Data,Zscore(Data.copy()))方差: 51.569160680908254
Z-score标准化后的矩阵是 [[0.2 0.9 0.13864876]
[0.9 0.1 1.5154406 ]
[0.5 0.5 0.15804019]]
3.4 局限
- 对样本量少的数据,表现不好
- 标准化后范围在有负有正,范围在[-1,1]
4 小数定标法
4.1 公式
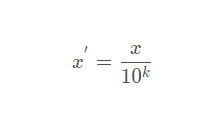
4.2 算法实现逻辑
- 输入数据
- 绝对值化,最大值
- 将每个数除以最大值的数量级
- 输入数据
4.3 代码实现
# 小数定标归一化算法
def Decimals(data):
C = np.abs(data[:,2])
max = int(np.sort(C)[-1]) # 按从小到大排序,取最后一位,及最大值
k = len(str(max))
print('绝对值最大的位数:\n',k)
data[:2] = data[:,2] /(10**k)
print('小数点定标准化后的矩阵:\n',data)
return data
ShowData(Data,Decimals(Data.copy()))绝对值最大的位数:
3
小数点定标准化后的矩阵:
[[2.9e-02 1.0e-01 3.0e-02]
[2.9e-02 1.0e-01 3.0e-02]
[5.0e-01 5.0e-01 3.0e+01]]
4.4 局限
- 受到最大值影响较大
到此这篇关于Python实现归一化算法详情的文章就介绍到这了,更多相关Python归一化算法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
相关文章

如何用Python Beautiful Soup解析HTML内容
Beautiful Soup是一种Python的解析库,主要用于解析和处理HTML/XML内容,详细介绍Beautiful Soup的使用方式和应用场景,本文给大家介绍的非常详细,需要的朋友可以参考下2023-05-05
Python phone模块获取手机号归属地 区号 运营商等信息demo
这篇文章主要介绍了Python phone模块获取手机号归属地 区号 运营商等信息的实现示例,有需要的朋友可以借鉴参考下,希望能够有所帮助,祝大家多多进步,早日升职加薪2023-05-05












最新评论