Python实现arctan换算角度的示例

笛卡尔坐标系

对于平面坐标系，任一射线OP与x轴夹角θ的范围，可以取[0,2π)或者(-π,π]，如无特殊说明， 我们统一使用后者。
将笛卡尔空间坐标系中的点 Pc = ( x , y , z ) 表示成球体坐标系中的形式 Ps = ( θ , ϕ , r )。

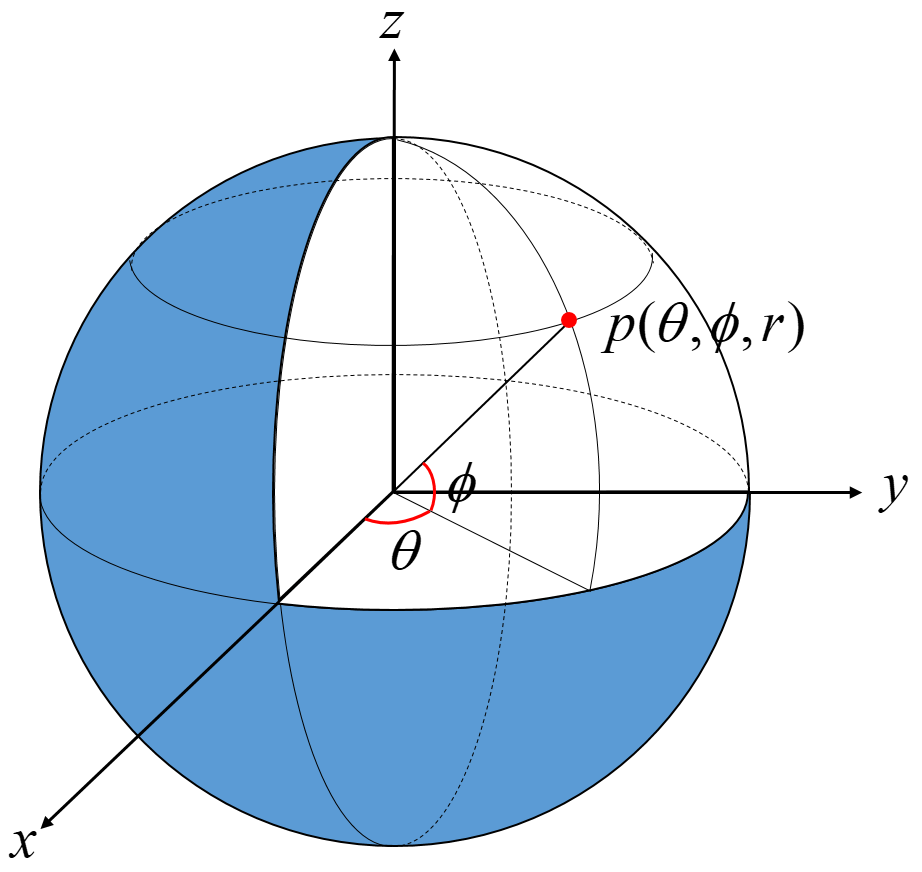
其中

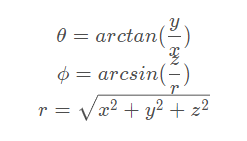
根据球坐标的定义，要求θ∈[−π,π]，ϕ∈[−π/2,π/2] ，r∈[0 , +∞)。

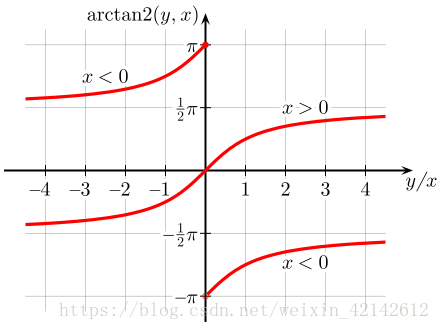
对于 θ，正切函数的周期是 π，因此反正切函数 arctan 一般也只取一个周期，其定义域是 R，值域是(−π/2 , π/2) 。为了解决这个问题，引入了 Arctan 函数，也就是 arctan2 函数。

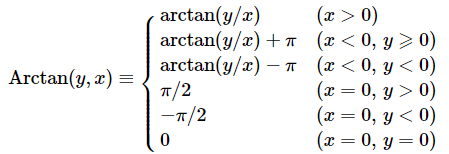
atan2 函数的使用 atan2(delta_y , delta_x)

import math
a = math.atan2(400,-692.820)
# 2.6179936760992044
angle = a/math.pi*180
# 149.99998843242386

atan 函数的使用 atan(delta_y / delta_x)

import math
delta_y = 400
delta_x = -692.820

if delta_x == 0:
    b = math.pi / 2.0
    angle = b/math.pi*180
    if delta_y == 0:
        angle = 0.0
    elif delta_y < 0:
        angle -= 180
else:
    b =  math.atan(delta_y/delta_x) 
    angle = b/math.pi*180
    if delta_y > 0 and delta_x < 0:
        angle = angle + 180
    if delta_y < 0 and delta_x < 0:
        angle = angle - 180

b,angle
# (-0.5235989774905888, 149.99998843242386)

atan 和 atan2 的异同

• 参数的个数不同
• 两者返回值都是弧度
• 如果 delta_x等于0，atan2依然可以计算，但是 atan 则需要提前判断，否则就会导致程序出错
• 象限的处理

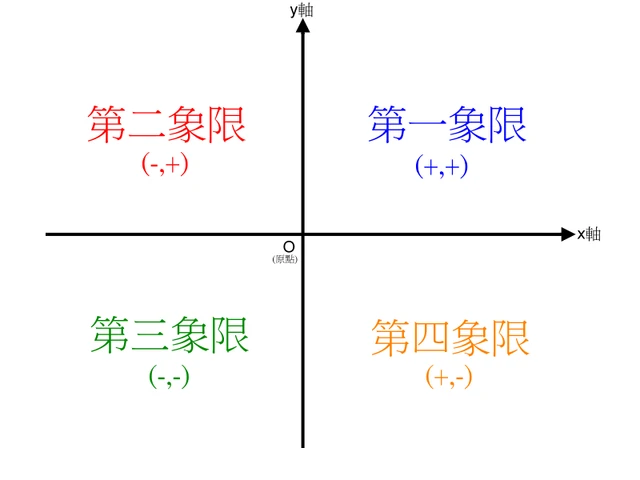
atan2(b,a)是4象限反正切，它的取值不仅取决于正切值b/a，还取决于点(b,a) 落入哪个象限：

• 当点 (b,a) 落入第一象限(b>0, a>0)时，atan2(b,a)的范围是 0 ~ pi/2
• 当点 (b,a)落入第二象限(b>0, a<0)时，atan2(b,a)的范围是 pi/2 ~ pi
• 当点 (b,a)落入第三象限(b<0, a<0)时，atan2(b,a)的范围是 -pi～-pi/2
• 当点 (b,a) 落入第四象限(b<0, a>0)时，atan2(b,a)的范围是 -pi/2～０

而 atan(b/a) 仅仅根据正切值为a/b求出对应的角度 (可以看作仅仅是2象限反正切)：

• 当 b/a > 0 时，atan(b/a)取值范围是 0 ~ pi/2
• 当 b/a < 0 时，atan(b/a)取值范围是 -pi/2～0

取值范围

• 点 (b,a) 落入第一象限 (b>0, a>0)或 第四象限(b<0, a>0)时，atan2(b,a) = atan(b/a)
• 点 (b,a) 落入第二象限 (b>0, a<0)，b/a<0，故atan(b/a)取值范围始终是 -pi/2～０，然而，atan2(b,a)的范围是 pi/2 ~ pi，故atan(b/a) 计算角度值要加180。
• 点 (b,a) 落入第三象限(b<0, a<0) ，b/a>0，故 atan(b/a) 取值范围是 0 ~ pi/2，而此时atan2(b,a)的范围是 -pi～-pi/2，故atan(b/a) 计算角度值要减180。

结论： atan 和 atan2函数，建议用 atan2函数

到此这篇关于Python实现arctan换算角度的示例的文章就介绍到这了,更多相关Python arctan换算角度内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！

最新评论