python使用回溯算法实现列表全排列
python使用回溯算法实现列表全排列
问题:输入列表L(不含重复元素),输出L的全排列。
如输入:L=[1,2,3]
则输出:[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
全排列问题,可以用回溯法解决,详细分析请参考东哥公众号:labuladong,看了之后醍醐灌顶。
先帖一个正确解法:
'''
回溯算法模板:
from: labuladong公众号
result = []
def backtrack(选择列表,路径):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择(要去重,判断该选择是否已经在选择列表中,已经选过的不要选)
backtrack(选择列表,路径)
选择列表.removelast() #撤销这个选择,因为要重新从头开始(回溯树的跟节点)
'''
import copy
def backtrack(L,path):
if len(path)==len(L):
c = copy.copy(path) # 注意这里不是直接将path加到res中,而是深拷贝了一个对象
res.append(c)
# res.append(path)
# print(res)
return
for i in L:
if i in path:
continue
else:
path.append(i)
backtrack(L,path)
#path = path[:-1]
path.pop() # 注意此处“撤销”选择的方法
if __name__ == '__main__':
res = []
L = [1,2,3]
backtrack(L,[])
print(res)输出:

以上算法使用python的深拷贝,假如不使用会怎样呢?
看下面代码:
def backtrack(L,path):
if len(path)==len(L):
# c = copy.copy(path)
# res.append(c)
res.append(path)
print(res)
return
for i in L:
if i in path:
continue
else:
path.append(i)
backtrack(L,path)
#path = path[:-1]
path.pop() # 注意此处“撤销”选择的方法
if __name__ == '__main__':
res = []
L = [1,2,3]
backtrack(L,[])
print(res)此时的输出:

这个结果着实令人疑惑, 仔细分析后发现是python的浅拷贝搞的鬼。当我们判断len(path) == L时,就将path append到res中,但事实上,res中存放的只是path的一个指针,当我们对path进行“撤销选择”时,即path.pop(),会连带着将res中元素也修改掉,这显然是不合理的。仔细看的话其实每一次输出的第一列组合起来刚好是全排列。
再看一个错误示例,在撤销选择时不适用path.pop(),而是path = path[:-1]。
import copy
def backtrack(L,path):
if len(path)==len(L):
c = copy.copy(path) # 注意这里不是直接将path加到res中,而是深拷贝了一个对象
res.append(c)
# res.append(path)
print(res)
return
for i in L:
if i in path:
continue
else:
path.append(i)
backtrack(L,path)
path = path[:-1] # 换一种“撤销”选择的方法
#path.pop() # 注意此处“撤销”选择的方法
if __name__ == '__main__':
res = []
L = [1,2,3]
backtrack(L,[])
print(res)此时的输出:

更加令人疑惑,使用debug调试后发现,path撤销选择,即path = path[:-1]没起到作用,在向上回溯的过程中,由于函数签名是
backtrack(L,path)
由于path是以一个参数的形式传入函数的,所以每一层递归调用中,使用的path应该是同一个,当我们用path.pop()撤销选择时,每一层的递归栈中,path应该同时发生变化。(可以这么类比,当我第一轮递归,path=[1,2,3]后,向上递归时,合理思考应该将path依次变成[1,2]、[1],这样才能继续向里面添加元素,组成不同的排列),但使用path = path[:-1],调试发现除了本层递归栈以外,其他递归栈的path并未发生变化:
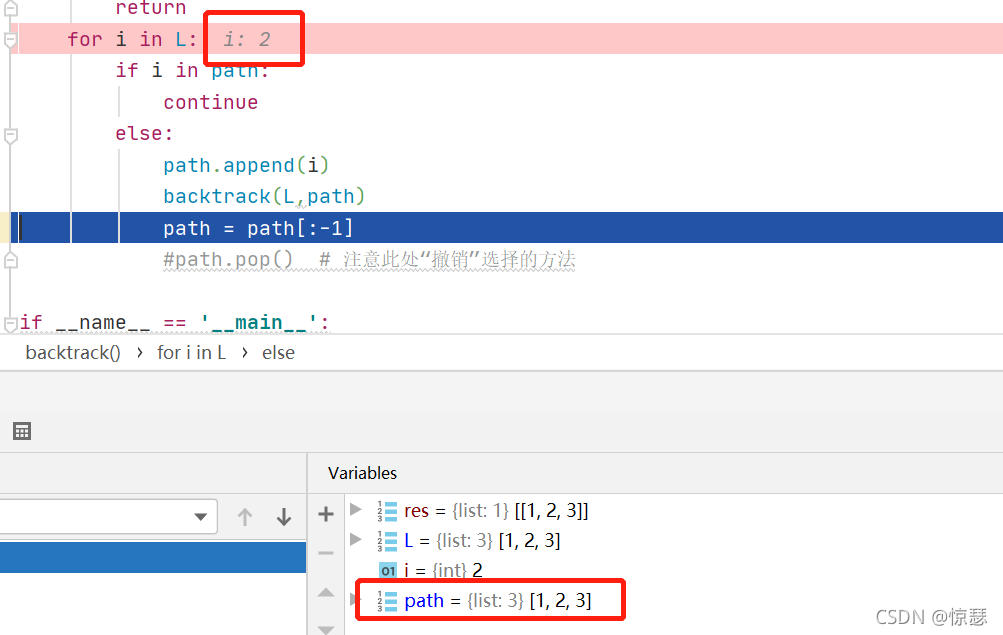
这次是深拷贝的锅,我们合理怀疑path=path[:-1],应该是生成了一个新的对象,即=左右的path并不是同一个对象,因此每层递归树的path不会改变,来验证一下:

破案了。
到此这篇关于python使用回溯算法实现列表全排列的文章就介绍到这了,更多相关python列表全排列内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
相关文章

python+pytest接口自动化之日志管理模块loguru简介
python中有一个用起来非常简便的第三方日志管理模块--loguru,不仅可以避免logging的繁琐配置,而且可以很简单地避免在logging中多进程多线程记录日志时出现的问题,甚至还可以自定义控制台输出的日志颜色,接下来我们来学习怎么使用loguru模块进行日志管理2022-05-05
python 时间 T 去掉 带上ms 毫秒 时间格式的操作
这篇文章主要介绍了python 时间 T 去掉 带上ms 毫秒 时间格式的操作,具有很好的参考价值,希望对大家有所帮助。一起跟随小编过来看看吧2021-04-04












最新评论