Java面试之动态规划与组合数

最近在刷力扣上的题目，刷到了65不同路径，当初上大学的时候，曾在hihocoder上刷到过这道题目，但是现在已经几乎全忘光了，大概的知识点是动态规划，如今就让我们一起来回顾一下。

从题目说起

题目原文是：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

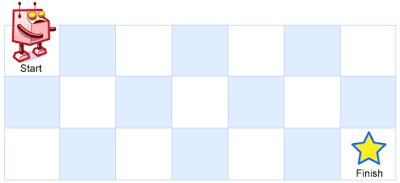
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2

输出: 3

解释:

从左上角开始，总共有 3 条路径可以到达右下角。

向右 -> 向右 -> 向下
向右 -> 向下 -> 向右
向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3

输出: 28

正向思路

我们先按照正常思路来想一下，当你处于起点时，你有两个选择，向右或者向下，除非你处于最下面一排或者最右边一列，那你只有一种选择（比如处于最下面一排，你只能往右），其他位置，你都有两种选择。

因此，我们就根据这个思路，可以写出代码：

class Solution {
  public int uniquePaths(int m, int n) {
    // 特殊情况：起点即终点
    if (m == 1 && n == 1) {
      return 1;
    }
    // 当前处于(1,1)，终点为(m,n)
    return walk(1, 1, m, n);
  }
  public int walk(int x, int y, int m, int n){
    // 已经处于终点
    if (x >= m && y >= n) {
      return 0;
    }
    // 处于最下面一排或者最右边一列
    if (x >= m || y >= n) {
      return 1;
    }
    // 往下走，有多少种走法
    int down = walk(x, y + 1, m, n);
    // 往右走，有多少种走法
    int right = walk(x + 1, y, m, n);
    // 从当前(x,y)出发，走到(m,n)，共有多少种走法
    return down + right;
  }
}

优化

我们考虑一下，这种写法，有没有可以优化的地方。

你们应该一眼就发现，walk方法的第一个判断if (x >= m && y >= n)，永远都不可能为true，因为下一个判断if (x >= m || y >= n)就已经是临界点情况，直接就已经有返回值，根本不可能达到x >= m && y >= n的情况。因此，该判断可以删除。

假设我们从(1,1)的位置出发，终点是(3,3)，那么到达(2,2)这个中间点的话有几种走法呢？两种，先到(1,2)再到(2,2)，或者，先到(2,1)再到(2,2)。

因此，如果根据我们上面的写法，从(2,2)到终点(3,3)，我们会算两次，虽然这样的思路本身是正确，但这样的情况应该是可以优化的。因为从(1,1)到(3,3)，一共只有6种路径，但已经有2条是重复的路径了，那么随着m与n越来越大，中间点会越来越多，那么重复的路径也会越来越多。

这就是前面的选择对于后面的选择会有影响，即使后面的选择相同，但由于前面的选择不同，从而也被认为是不同的选择。

很明显，后面的选择更加唯一，如果我们先在后面做出选择，那么就可以减少重复计算的次数。因此，我们可以试试反向思路。

反向思路

如果我们不是从起点出发，而是从终点倒退到起点开始算的话。假设终点是(3,3)，它只能由(2,3)和(3,2)直接到达，(2,3)也只能由(2,2)和(1,3)直接到达，(1,3)只能由(1,2)直接到达，(1,2)只能由(1,1)直接到达，因此(1,3)只能由(1,1)直达。

我们可以得出规律：除了最左边一列和最上面一排的点，只能由起点(1,1)直达以外，其他的点(x,y)都是由(x-1,y)和(x,y-1)两个点直接到达的。

因此，根据这个思路，我们可以写出代码：

class Solution {
  public int uniquePaths(int m, int n) {
    int[][] result = new int[m][n];
    int j;
    for (int i = 0; i < m; i++) {
      for (j = 0; j < n; j++) {
        if (i == 0 || j == 0) {
          // 最上面一排的点和最左边一列的点，只能由(1,1)到达
          result[i][j] = 1;
        } else {
          // 其他的点都可以由左边的点和上面的点到达
          result[i][j] = result[i - 1][j] + result[i][j - 1];
        }
      }
    }
    return result[m - 1][n - 1];
  }
}

其实这样的想法就已经是动态规划的范畴了，我们看看维基上的定义

动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

一开始我感觉很像分治法，因为都需要将一个大问题分解为子问题，但分治法最终会将子问题合并，但动态规划却不用。

优化

我们考虑一下，这种写法，有没有可以优化的地方。

首先是空间上的优化，我们一定要用二维数组吗？可以用一维数组代替吗？

答案是肯定的，因为每个点的计算只和左边与上边相邻的点有关，因此，不需要更加久远的点。

一维数组

假如只用一维数组，那么只需要存储上一排的结果，如果计算到下一排的时候，则依次替换，代码为：

class Solution {
  public int uniquePaths(int m, int n) {
    int[] dp = new int[m];
    int j;
    for(int i = 0; i < n; i++) {
      for(j = 0; j < m; j++) {
        if(j == 0) {
          dp[j] = 1;
        }
        else {
          // 其他的点都可以由左边的点和上面的点到达
          dp[j] += dp[j-1];
        }
      }
    }
    return dp[m-1];
  }
}

这样的优化，差不多就结束了。那我们是否可以从思路上进行优化呢？

组合数

因为我们只有向右或向下两种选择，而我们一共要走的路径其实是(m-n-2)，其中有(m-1)的路径是向右，(n-1)的路径是向下，其实可以转变为：

从(m-n-2)中挑出(m-1)，即组合数C((m-n-2), (m-1))的值

那么我们可以写出代码：

class Solution {
  public int uniquePaths(int m, int n) {
    // 用double，因为计算出的数值会很大
    double num = 1, denom = 1;
    // 找出更小的数，这样可以减少计算次数和计算出的数值
    int small = m > n ? n : m;
    for (int i = 1; i <= small - 1; ++i) {
      num *= m + n - 1 - i;
      denom *= i;
     }
     return (int)(num / denom);
  }
}

总结

以上所述是小编给大家介绍的Java面试之动态规划与组合数,希望对大家有所帮助，如果大家有任何疑问请给我留言，小编会及时回复大家的。在此也非常感谢大家对脚本之家网站的支持！
如果你觉得本文对你有帮助，欢迎转载，烦请注明出处，谢谢！

最新评论