Java实现动态规划背包问题
前言
给定 n n n 种物品和一个背包。物品 i i i 的重量是 w i wi wi,其价值为 v i vi vi,背包的容量为 c c c。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
一、原理
0 − 0 - 0− 1 1 1 背包问题是一个特殊的整数规划问题。
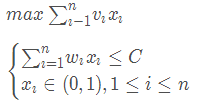
1.1 最优子结构性质
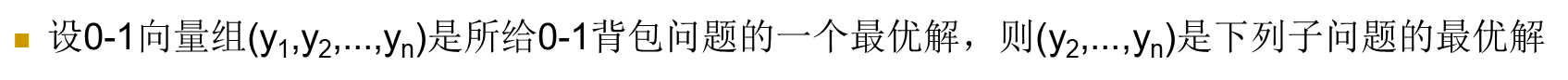
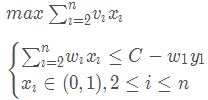
1.2 递归关系
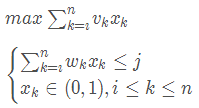
设所给 0 − 1 0-1 0−1 背包问题的子问题的最优值为 m(i,j),即 m(i,j)是背包容量为 j,可选择物品为 i,i+1,…,n 时 0-1背包问题的最优值。由 0-1背包问题的最优子结构性质,可以建立计算 m(i,j)的递归式如下:
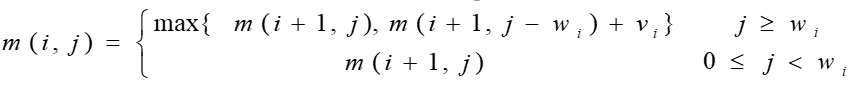
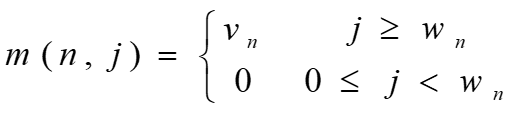
二、算法描述
2.1 算法描述
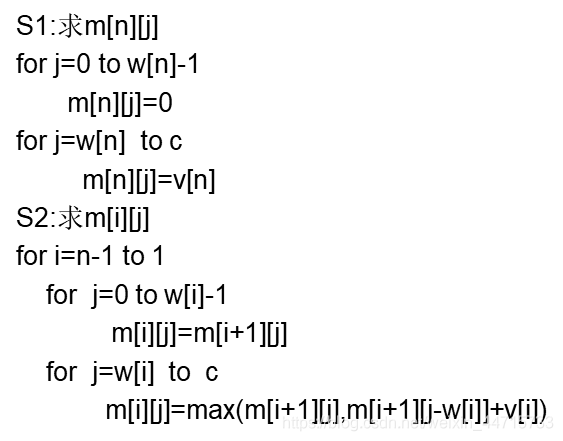
伪代码:

2.2 图解

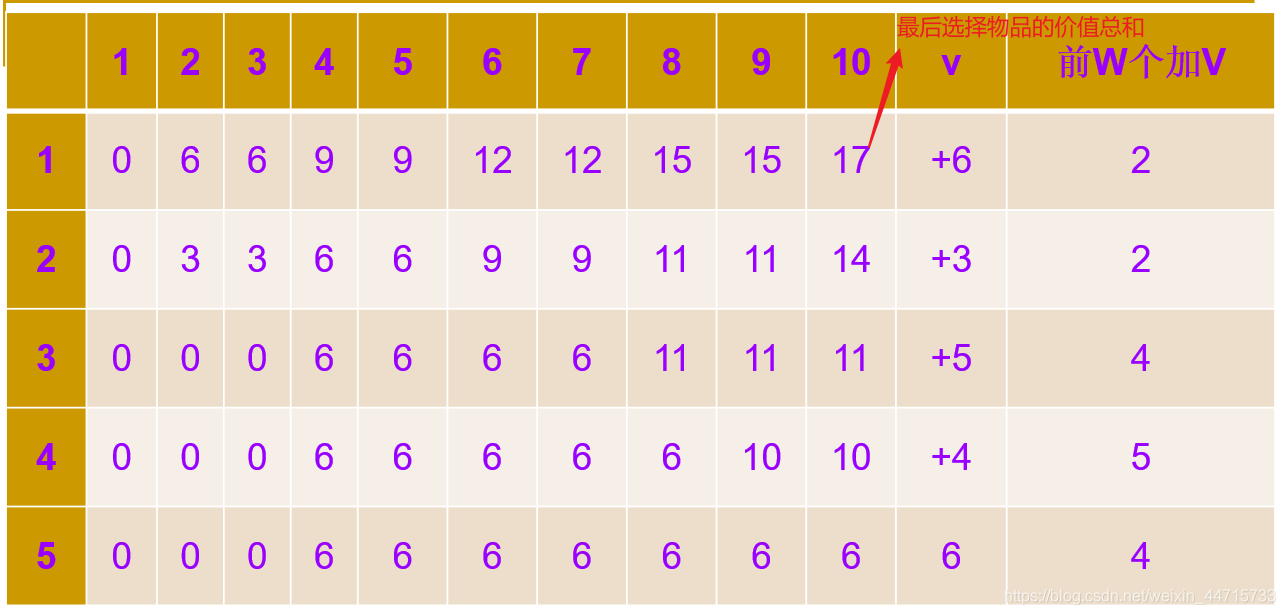
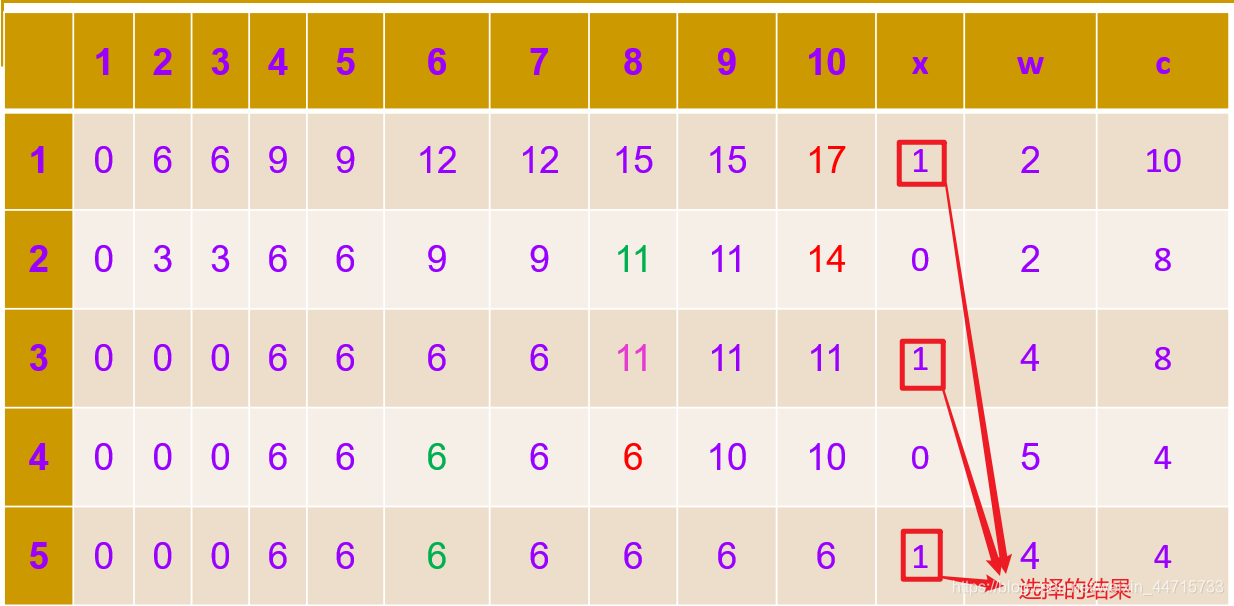
2.3 构造最优解

三、 0 − 1 0-1 0−1 背包问题相关题目
3.1 题目
已知有5个物体,它们的重量分别为:2,2,4,5,4,各物体的价值依次为6,3,5,4,6,背包大小为10,使用动态规划法求矩阵m[i][j],并给出最优解。修改数据为:5个物体,它们的重量分别为:1,1,2,3,2,各物体的价值依次为6,3,5,4,6,背包大小为6,使用动态规划法求矩阵m[i][j],并给出最优解
3.2 源程序(Java求解 0 − 1 0-1 0−1背包问题)
/**
* 0-1背包问题(动态规划法求解)
*/
public class E3_9 {
//物品的个数+1(第一个数我写成0)
static int N = 6;
//static int C = 7;
static int C = 11;
/**
* 程序的入口
* @param args
*/
public static void main(String[] args) {
//int n = N-1;
//背包的容量
int c = C-1;
int i;
//物体的重量
//int w[] = new int[N];
int w[] = new int[]{0,2,2,4,5,4};
//int w[] = new int[]{0,1,1,2,3,2};
//物体的价值
//int v[] = new int[N];
int v[] = new int[]{0,6,3,5,4,6};
//动态规划法求解过程的矩阵
int m[][] = new int[N][C];
//选择的结果
int x[] = new int [N];
// for (i = 1; i < N; i++) {
// w[i] = 1+(int) (Math.random()*5);
// v[i] = 1+(int) (Math.random()*10);
// }
knapsack(v,w,c,m);
traceback(m,w,c,x);
System.out.printf("背包能装的最大价值为:"+"%d \n ",m[1][c]);
for (i = 1; i <= c; i++) {
System.out.printf("%2d \t",i);
}
System.out.printf("重量 价值\n");
for (i = 1; i < N; i++) {
System.out.printf("%d:",i);
for (int j = 1; j <= c; j++) {
System.out.printf("%2d \t",m[i][j]);
}
System.out.printf("%2d%4d\n",w[i],v[i]);
}
System.out.printf("\n\n物品的重量");
for (i = 1; i < N; i++) {
System.out.printf("%2d \t",w[i]);
}
System.out.printf("\n物品的价值");
for (i = 1; i < N; i++) {
System.out.printf("%2d \t",v[i]);
}
System.out.printf("\n选择的结果");
for (i = 1; i < N; i++) {
System.out.printf("%2d \t",x[i]);
}
System.out.printf("\n");
}
/**
* 由0-1背包问题的最优子结构性质建立的递归式
* @param v 存储物品价值的数组
* @param w 存储物品重量的数组
* @param c 背包容量
* @param m 动态规划法求解过程的矩阵
*/
public static void knapsack(int []v,int []w,int c,int [][]m){
int n=v.length-1;
int jMax=Math.min(w[n]-1,c);
for(int j=0;j<=jMax;j++) m[n][j]=0;
for(int j=w[n];j<=c;j++) m[n][j]=v[n];
for(int i=n-1;i>0;i--){
jMax=Math.min(w[i]-1,c);
for(int j=0;j<=jMax;j++)
m[i][j]=m[i+1][j];
for(int j=w[i];j<=c;j++)
m[i][j]=Math.max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
}
//m[1][c]=m[2][c];
//对于i=1时的两种情况
if(c>=w[1])
m[1][c]=Math.max(m[2][c],m[2][c-w[1]]+v[1]);
else
m[1][c]=m[2][c];
}
/**
* 构造最优解
* @param m 动态规划法求解过程的矩阵
* @param w 存储物体的重量的数组
* @param c 背包容量
* @param x 存储选择结果的数组
*/
public static void traceback(int [][]m,int []w,int c,int []x){
int n=w.length-1;
for(int i=1;i<n;i++)
if(m[i][c]==m[i+1][c])
x[i]=0;
else {
x[i]=1;
c-=w[i];
}
x[n]=(m[n][c]>0)?1:0;
}
}
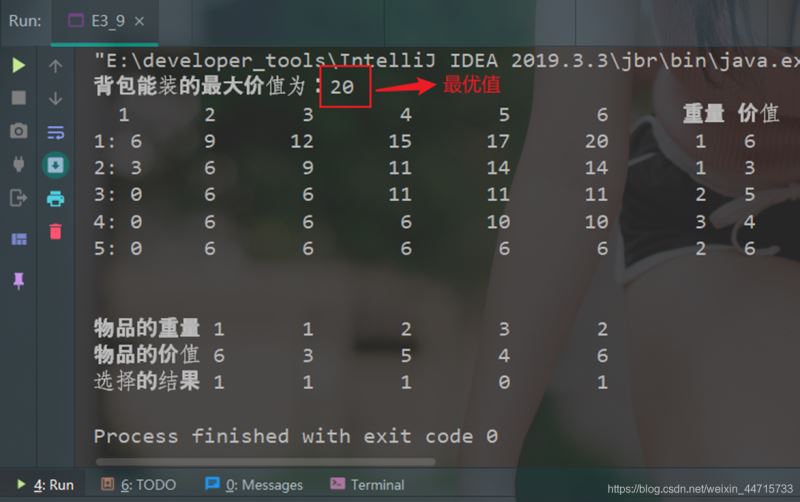
3.3 运行结果

总结
动态规划基本步骤
- 找出最优解的性质,并刻划其结构特征。
- 递归地定义最优值。
- 以自底向上的方式计算出最优值。
- 根据计算最优值时得到的信息,构造最优解。
到此这篇关于Java实现动态规划背包问题的文章就介绍到这了,更多相关java动态规划内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
相关文章

java开发RocketMQ之NameServer路由管理源码分析
这篇文章主要为大家介绍了java开发中RocketMQ之NameServer路由管理源码分析详解,有需要的朋友可以借鉴参考下,希望能够有所帮助,祝大家多多进步早日升职加薪2021-11-11
Spring Boot 中的 @DateTimeFormat 和 @JsonFormat 的用法及作用详解
本文介绍了SpringBoot中的@DateTimeFormat和@JsonFormat注解的用法,解释了它们在处理日期和时间数据时的作用,并通过实例代码展示了如何在REST控制器中使用这些注解,感兴趣的朋友跟随小编一起看看吧2024-11-11
解读SpringBoot中addCorsMappings配置跨域与拦截器互斥问题的原因
这篇文章主要介绍了解读SpringBoot中addCorsMappings配置跨域与拦截器互斥问题的原因,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教2023-12-12












最新评论